Roll Variance in the Bearoff - Part 2
by Douglas Zare
8 October 2014

Each extra pip was worth about 0.127, while each extra unit of roll variance costs 0.317, or about 2.5 pips. What happens if you vary the position of the roller?
Let's do the same analysis for other positions with about the same effective pip count of 52, but different roll variances for the leader.
| | ||
| | ||
| | ||
| | ||
| | ||
| | ||
These positions have epcs of 51.984. 51.943, and 51.952, respectively. These are within a twentieth of a pip, so if you just go by the epcs, you might expect the equities after Double/Take to be extremely close. Because the roll variances differ greatly, the equities in EMG are 1.025, 0.967, and 0.870, respectively, when White takes.
The best linear fit for the equity of Double/Take in position A2 for positions with epcs between 54 and 58 is -5.978 + 0.132 epc - 0.378 rv. In other words, a position with an effective pip count of 56 with a roll variance of 1 would have an equity estimated at 1.054. Each extra pip for the taker is worth 0.132, and each unit of roll variance is worth 2.857 pips.
The best linear fit in position B2 (closed board) was in part 1: -5.838 + 0.127 epc - 0.317 rv. A position with an effective pip count of 56 with a roll variance of 1 would have an equity estimated at 0.983. Each extra pip is worth 0.127, and each unit of roll variance is worth 2.490 pips.
The best linear fit in the efficient position C2 is -5.937 + 0.126 epc - 0.237 rv. A position with an epc of 56 and roll variance of 1 would have an equity estimated at 0.865. Each extra pip is worth 0.126, and each unit of roll variance is worth 1.884 pips.
| Position | Best linear fit | Equity | Pip -> EMG | RV -> Pip |
| A2 | -5.978 + 0.132 epc - 0.378 rv | 1.054 | 0.132 | 2.857 |
| B2 | -5.838 + 0.127 epc - 0.317 rv | 0.983 | 0.127 | 2.490 |
| C2 | -5.937 + 0.126 epc - 0.237 rv | 0.865 | 0.126 | 1.884 |
The value of a pip didn't change much, but the base equity changed, as did the importance of roll variance. If the doubler has an efficient position with high roll variance, then roll variance is less important to the trailer. If the doubler has a position closer to a pure n-roll position with low roll variance, then roll variance is more important to the trailer.
Based on these estimates, here are the borderline take/pass combinations of roll variance and effective pips for positions A2, B2, and C2:
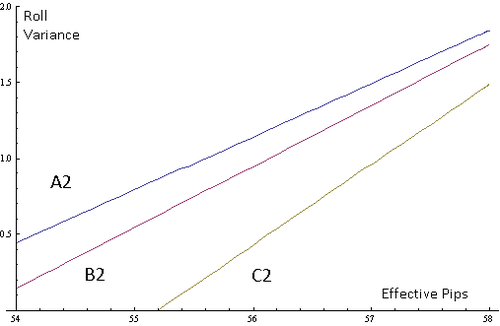
One way to get information from this graph is by imagining a horizontal line at some roll variance. The distance between the intersections with the line for A2 and with C2 is about 2 pips if the horizontal line is low, and about 1 pip if the horizontal line is high. This means a higher roll variance for the leader, having position C2 instead of C1, costs the leader about 2 pips if the trailer has a low roll variance, but only 1 pip if the trailer has a high roll variance.
Shorter Races
Here are some positions with epcs close to 32:
| | ||
| | ||
| | ||
| | ||
| | ||
| | ||
Even though Red's effective pip counts were all close to 31.9, the equities of Double/Take were 1.159, 1.010, and 0.913.
Here are the best fits when the trailer has an effective pip count between 32.5 and 35.5, estimated equities against a position with an effective pip count of 34 and a roll variance of 0.5, values of a pip in EMG, and values of a unit of roll variance in pips for these position.
| Position | Best linear fit | Equity | Pip -> EMG | RV -> Pip |
| A1 | -3.394 + 0.142 epc - 0.577 rv | 1.145 | 0.142 | 4.063 |
| B1 | -4.025 + 0.154 epc - 0.416 rv | 1.017 | 0.154 | 2.694 |
| C1 | -4.040 + 0.151 epc - 0.316 rv | 0.934 | 0.151 | 2.095 |
We see the same general pattern as before: When the leader has a higher roll variance, the trailer is in better shape, and roll variance is less important to the trailer. Each unit of roll variance is worth more when the race is short, but it is also harder for a position to have a high roll variance in a short race.
Here are the borderline take/pass combinations of roll variance and effective pips. Although the graph shows roll variances from 0 to 2 for comparability with the graphs for longer races, the actual feasible range is 0.418-0.844.
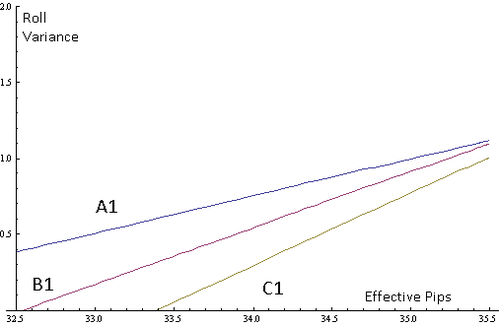
The horizontal distance between C1 and A1 is about 2 pips for low trailer roll variances, and about 1 pip for high trailer roll variances.
Longer Races
Here are positions with epcs close to 72 with a range of roll variances:
| | ||
| | ||
| | ||
| | ||
| | ||
| | ||
The equities in these positions are 1.037, 1.001, and 0.919, respectively.
Here are the best fits when the trailer has an effective pip count between 76.6 and 80.6, estimated equities against a position with an effective pip count of 78 and a roll variance of 1.0, values of a pip in EMG, and values of a unit of roll variance in pips for these position.
| Position | Best linear fit | Equity | Pip -> EMG | RV -> Pip |
| A3 | -6.553 + 0.101 epc - 0.226 rv | 1.107 | 0.101 | 2.233 |
| B3 | -6.348 + 0.097 epc - 0.200 rv | 1.055 | 0.097 | 2.052 |
| C3 | -6.402 + 0.096 epc - 0.172 rv | 0.953 | 0.096 | 1.782 |
This confirms the pattern that when the leader has a higher roll variance, the trailer is better off, and it is less important for the trailer to have a high roll variance.
Here is a graph showing the estimated borderline take/pass combinations when the leader has one of these positions and doubles.
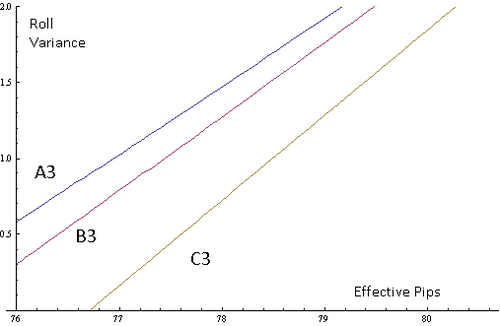
It appears that in longer races, the roll variance matters less per unit, but there are larger differences between the highest roll variances and the lowest, although those differences decrease as you approach 90 pips. The difference betwen C3 and A3 is about 1.5 pips for a trailer with the lowest roll variance in this range, about 1.323 units. The highest possible roll variance is a little off the top of the graph at 2.135 units, and the difference between C3 and A3 is about 1 pip for those efficient positions.
In future parts, we will look at a more general model and versions of roll variance which are usable over the board. We will reconcile what we have learned about roll variance with advice such as that misses matter more for the leader than the epc indicates, while working doubles matter more for the trailer.
Copyright Douglas Zare and GammonVillage.

